For this third and final write-up of the CTF ECW 2023 edition, I will address the resolution of another challenge in the crypto category which has the originality of mixing pwn and cryptography, I named “CryptoFlow”.

You can download the program here .

Discovery of the challenge

In this challenge we have access to a binary. We start by quickly disassembling it on IDA.

The program performs the following actions:

• It loads a 128-bit (16 bytes) key from a file “aes_ecb_key.txt” into a buffer that I named aes_key ( LoadKey function ).
• It loads the contents of a “flag” file , encrypts it using AES128 and displays the encrypted content ( SendEncryptedFlag function).
• It then encrypts all future inputs sent to it using the same key.

We quickly understand that our objective is to decipher the flag provided when launching the program.

Before you begin, it’s important to understand how the AES encryption algorithm works so you don’t get too confused. For this I recommend this video which shows how it works very well.

The vulnerability

By playing a little with the program, we realize that there is a flaw in the GetMessage function. In fact, it copies all the data sent to it into a buffer located in the .data segment without checking whether the size of said buffer (224 bytes) is exceeded. We can therefore create a buffer-overflow in the program’s segment .data .

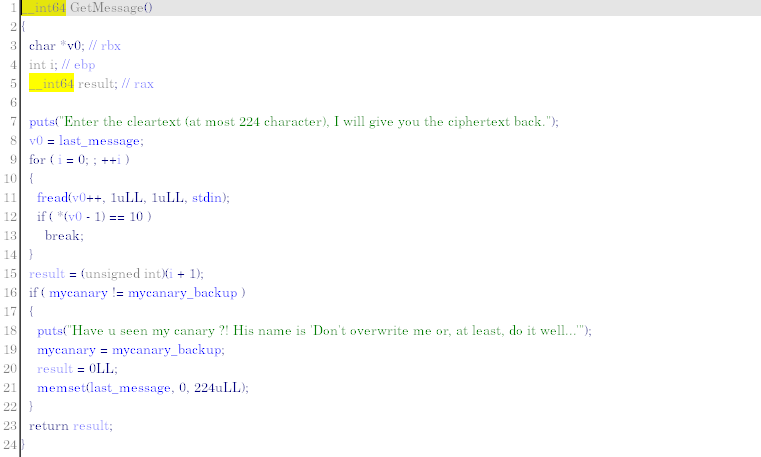
We are naturally interested in the data that we can overwrite in the .data segment in order to see what this flaw can allow us to do.

The data following the buffer storing the message to be encrypted is as follows:

• A 16-bit buffer called “mycanary  ” whose role is to check if there is buffer-overflow via a comparison with another buffer located further in the segment. However, as the value of this canary is fixed and known, the protection is not effective.
• After the canary we find a buffer of 256 bytes, called “s-box ”. This is a matrix allowing the proper functioning of the SubBytes cryptographic function in the AES algorithm.

We can therefore rewrite the S-BOX matrix by sending the following payload:

[224 bytes][MYCANARY=0xAABBCCDD00112233][S-BOX]

But what can happen if we change the value of the coefficients of the s-box matrix?

It is important to understand the role of this matrix within the AES. As said previously, this ensures the proper functioning of the SubBytes function . The SubBytes function performs a substitution operation on the coefficients of a column of a matrix. It associates a new value with each coefficient, following the following rule: for a coefficient of the form 0xAB, for example 0x19, it associates the value located at the A ^th line and B ^th column, i.e. 0xD4 for 0x19 .

Only if S-BOX is zero, then no matter how important the value of the coefficient is, its associated value will be zero. The result of SubBytes will therefore always be a zero matrix. This implies that at the output of the ShiftRows function , which follows SubBytes and whose role is to perform row swap operations, will have a zero output as well because swapping the rows of a null matrix will always result in a null matrix. The following function, AddRoundKey , which performs a term-to-term XOR operation between the State matrix and the roundkey will return the roundkey because A xor 0 = A. This implies that the result of our encryption will be equal to Roundkey #10 as we can see it in the image below.

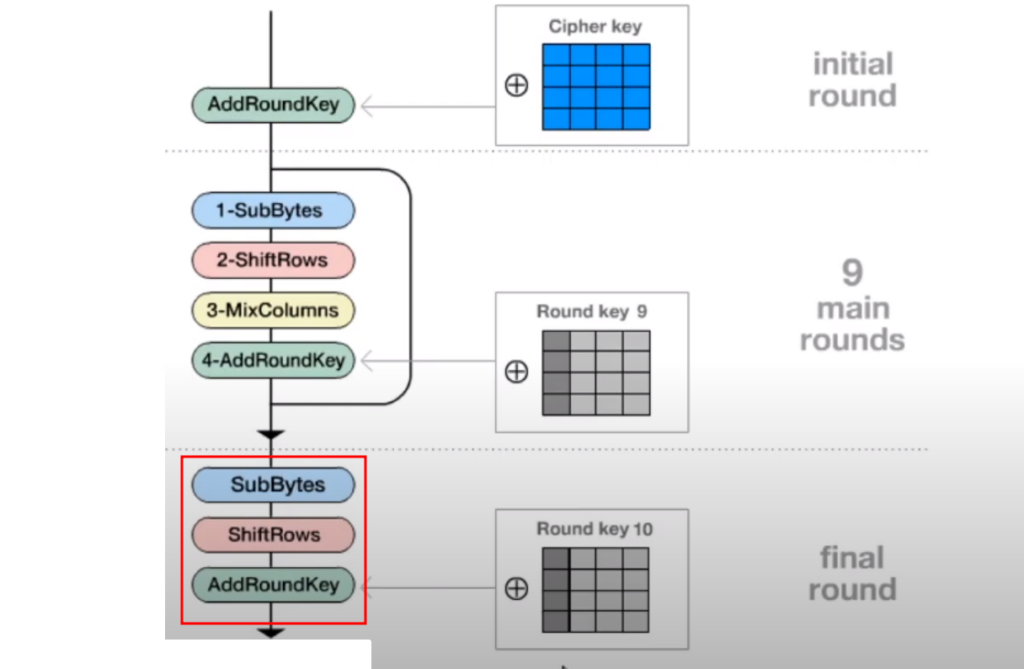
After encryption, we therefore obtain Roundkey n°10, the last of the Roundkeys. And it is very strong, because we can find the CipherKey, the main key, from an i ^th Roundkey, because the operations generating them are reversible.

Let’s go back to the code for the “main” function. We notice that there is a call to KeyExpension which is made before we overwrite S-BOX. This is a very important point, because it is the KeyExpension function which generates the 10 RoundKeys, and this uses the S-BOX matrix. All calls to KeyExpension which will be made after the S-BOX overwrite will generate keys which have lost the CipherKey information, i.e. unusable keys. It is therefore the result of the first encrypted message which is equal to the 10th ^RoundKey .

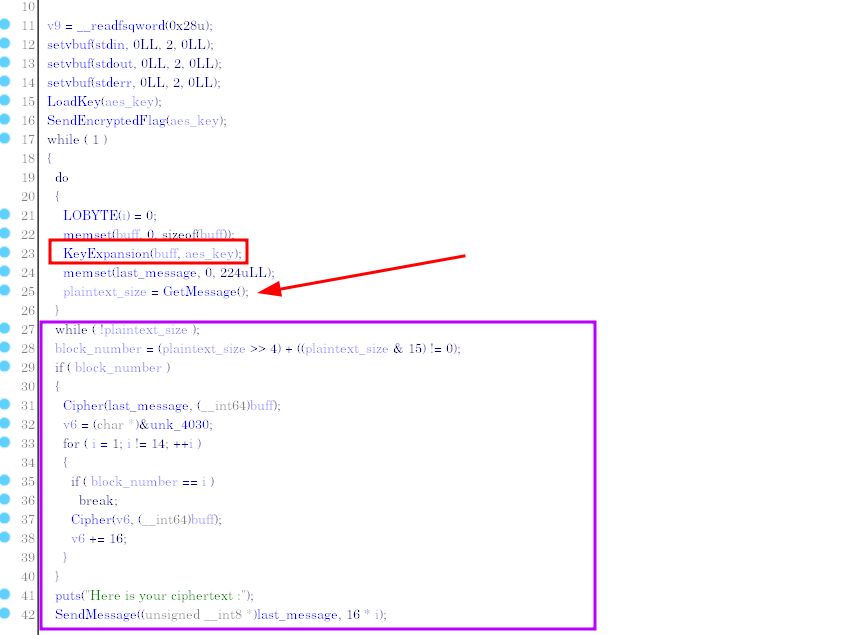
Reverse KeyExpension

I started by coding the function generating the i ^th Roundkey from the (i-1) ^th key.

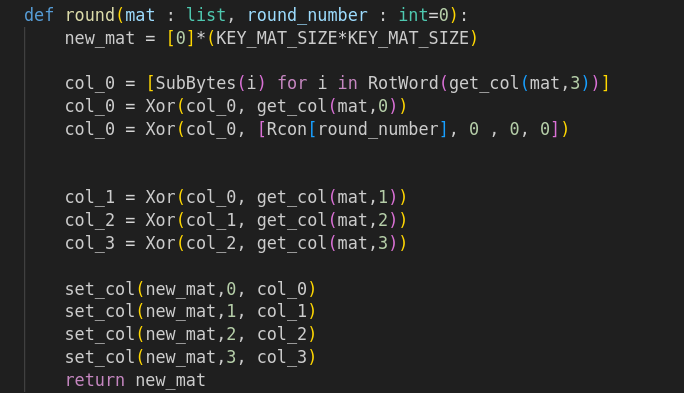
Then I coded its inverse function.

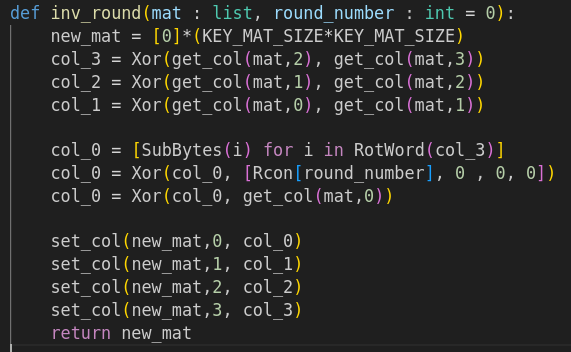
The full code is available on my github here (soon).

Now just run it to obtain the CipherKey and be able to decrypt the flag.