On approche du but : faire voler le drone (pour de vrai ce coup ci). Pour ce quatrième et dernier article de cette série, il nous faut nous intéresser à la stabilisation du drone. Dans cette partie je vais vous parler des différents capteurs que nous avons utilisé et comment utiliser leurs données pour asservir le drone (via un PID). Si vous n’avez pas lu l’article précédant (dans lequel on fait tourner les moteurs du drone), vous pouvez le retrouver ici.
Capteurs
Nous avons utilisé 2 capteurs :
– une centrale inertielle MPU6050, composée d’un capteur gyroscopique sur 3 axes et d’un accéléromètre sur 3 axes.
– un capteur de distance (plus précisément un télémètre à ultra-son) HC-SR04.
Nous aurions pu en utiliser un troisième capteurs, un magnétomètre pour aider au calcul des angles d’Euler.
NB: Je passe volontairement la partie configuration et récupération des données des capteurs pour l’instant, car ce n’est pas moi qui m’en suis occupé mais je vais essayer de la compléter prochainement.
Correcteur PID
Un peu de théorie
Le régulateur PID, appelé aussi correcteur PID est un système de contrôle permettant d’améliorer les performances d’un asservissement, c’est-à-dire un système ou procédé en boucle fermée. C’est le régulateur le plus utilisé dans l’industrie où ses qualités de correction s’appliquent à de multiples grandeurs physiques.
Wikipedia
En somme, il s’agit d’un concept de correcteur « efficace » qui va nous permettre d’assurer la stabilisation du drone. On l’intègre dans un système avec une boucle de rétroaction (système de correction d’erreur à rétroaction). Le principe est le suivant: on donne en entrée du système une consigne (un angle, par exemple 0° pour que le drone soit à l’horizontal), et ce dernier va calculer l’erreur par rapport à cette consigne (en utilisant les données fournies par les capteurs) via une boucle de retour. Ainsi, petit à petit, il va réduire cette erreur jusqu’à atteindre la valeur de la consigne le plus précisément possible.
Un correcteur PID est composé de 3 éléments: une composante proportionnelle (P), une composante intégrateur (I) et une dérivateur (D). Chacune de ses composantes à un rôle:
- Proportionnel: Son rôle est de pousser le système à atteindre la consigne. Il est proportionnel à l’erreur (le coefficient de proportionnalité étant [math]K_{P}[/math]. Cependant il génère une erreur statique : il s’agit d’une erreur que l’on conserve en régime permanent (après le régime transitoire, quand on est censé avoir atteint la consigne). En effet, plus on approche de la consigne, et donc du régime permanent, plus l’erreur est faible. Comme il s’agit d’un correcteur qui est proportionnel à l’erreur, son action s’en voit réduit, ce qui l’empêche d’atteindre la consigne avec précision et engendre une erreur. On peut l’observer sur l’image ci-dessous.
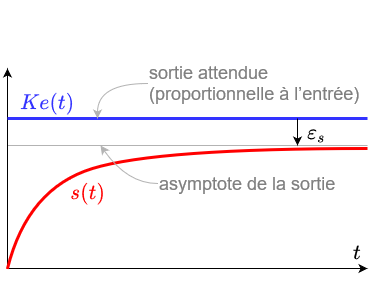
L’existence de cette erreur est démontrable par le calcul en utilisant le théorème de la valeur final, et est minimisé pour une entrée de type échelon en fixant la valeur de KP la plus grande possible. J’ai refait la démonstration ci-dessous (pour les amoureux des maths):
L’erreur [math]e(p)[/math] du système a pour expression (que l’on déduit du schéma block):
[math]e(p) = E(p)-R(p) = E(p)-e(p).FTBO(p)
\\\Leftrightarrow e(p) + e(p).FTBO(p) = E(p)
\\\Leftrightarrow e(p)(1+FTBO(p)) = E(p)
\\\Leftrightarrow e(p) = \frac{1}{1+FTBO(p)}.E(p) [/math]
Or le théorème de la valeur finale dit que : [math]E_{S} = \lim_{t \to \infty} e(t) = \lim_{p \to 0} p.e(p)[/math]. On peut considérer notre consigne d’entrée comme un échelon ayant comme amplitude la valeur de la consigne, donc d’après la transformée de Laplace on a [math] E(p) = A.\frac{1}{p} [/math]. Comme on considère un correcteur uniquement proportionnel on a [math] FTBO(p) = K_{p}[/math] donc en injectant les deux expressions on obtient: [math]E_{S} = \frac{1}{1+K_{p}}[/math]. Cette erreur est bien minimisé si [math]K_{p}[/math] est grand.
Seulement si on met un grande valeur pour [math]K_{p}[/math], on aura un dépassement de la consigne, ce qui entraîne des oscillations qui peuvent être gênantes dans notre cas. En effet, si on a des oscillations, on va accélérer puis décélérer successivement la vitesse des moteurs ce qui les abîmes. De plus, il nous est impossible d’annuler l’erreur statique complètement.
A noté que plus le coefficient [math]K_{p}[/math] est élevé, plus le système est rapide. - Intégrateur: L’intégrateur tient compte des erreurs précédentes. Il les additionnent (c’est pourquoi on parle d’intégration), jusqu’à ce que la consigne soit atteinte. Il permet de gagner en précision, en compensant l’erreur statique, et en stabilité.
On peut le démontrer mathématiquement : En rajoutant la transformé de Laplace d’un correcteur intégrateur dans notre expression on obtient [math]FTBO(p) = K_{P} + \frac{K_{I}}{p}[/math]. On a donc [math]E_{S} = \lim_{p \to 0} \frac{1}{1+K_{P} + \frac{K_{I}}{p}} = 0[/math].
Cependant on a toujours pas réglé le problème des dépassement. - Dérivateur: Le dérivateur permet de réduire voir d’éviter les dépassement (et donc les oscillations). Comme l’erreur au départ réduit rapidement (une pente abrupte), il aura une action négative qui freinera « fortement » l’évolution du système vers son état final. A l’inverse, lorsque l’évolution de l’erreur se stabilisera, son action sera quasiment nulle.
La difficulté réside dans le fait de trouver la bonne valeur pour ces 3 coefficients. La vidéo ci-dessous illustre bien l’influence du rôles des coefficients P, I et D.
On peut résumé le système du PID et du système de rétroaction au travers du schéma block ci-dessous :
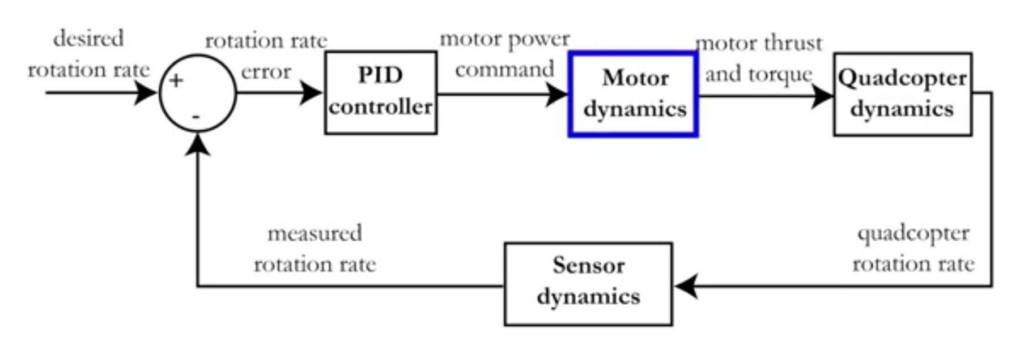
Où mathématiquement le PID équivaut à:
u(t) = K_{P}\times e(t) + K_{I} \times \int_0^t e(t) \mathrm{d}t + K_{D} \times \frac{e(t)}{dt}avec [math]K_{P}[/math], [math]K_{I}[/math] et [math]K_{D}[/math] les coefficients du PID qu’il nous faut déterminer. Dans le cadre de notre drone il va nous falloir utiliser plusieurs PIDs, 4 au total :
– Un PID pour chaque axe de rotation (pitch, roll et yaw)
– Un PID pour la distance par rapport au sol
Les plus importants étant les PIDs pitch et roll qui assure que le drone reste stable horizontalement.
En sortie des PIDs
En fonction de la valeur retourné par chacun des PIDs, il faut augmenter ou diminuer la valeur de la vitesse de certains moteurs.
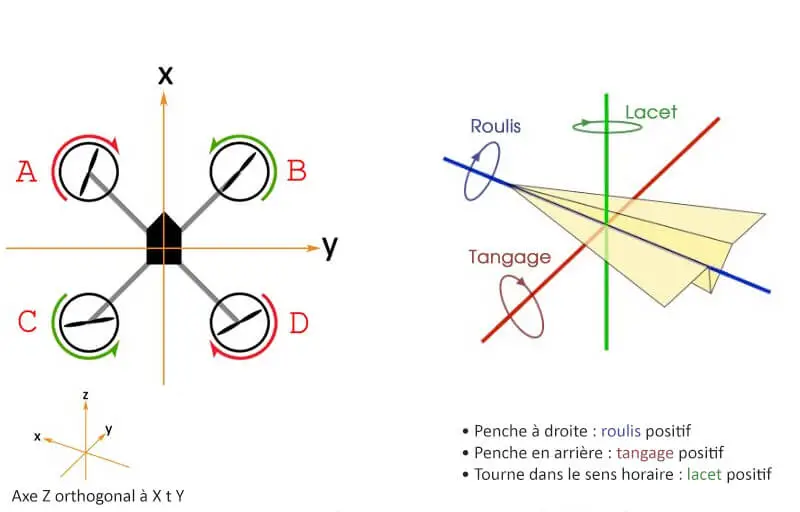
En réfléchissant un peu et en s’informant sur internet, on peut mettre au point un tableau d’action à prendre selon le cas auquel on est confronté. Lorsqu’on souhaite diminué ou augmenter la vitesse d’un moteur, on lui soustrait / ajoute la valeur en sortie du PID concerné. Vous pouvez trouver le tableau récapitulatif des actions à prendre en fonction des consignes ci-dessous:
| Consigne | Moteur 1 | Moteur 2 | Moteur 3 | Moteur 4 |
| Penche à droite (roulis positif) Translation vers la droite |  |  |  |  |
| Penche à gauche (roulis négatif) Translation vers la gauche |  |  |  |  |
| Penche en arrière (tangage positif) Translation vers l’arrière |  |  |  |  |
| Penche en avant (tangage négatif) Translation vers l’avant |  |  |  |  |
| Tourner dans le sens horaire (lacet positif) Rotation sens horaire |  |  |  |  |
| Tourner dans le sens antihoraire (lacet négatif) Rotation sens antihoraire |  |  |  |  |
Il ne nous reste plus qu’à adapter ça en code et faire des tests afin de déterminer la valeur des différents coefficients [math]K_{P}[/math], [math]K_{I}[/math] et [math]K_{D}[/math] des 4 PIDs.
NB : Comme les moteurs sont agencés en carré, les coefficients des axes pitch et roll sont les mêmes (donc plus que 9 coefficients à déterminer.
Déterminer les coefficients du PID
Pas le choix, il nous faudra déterminer ces coefficients expérimentalement, ce qui implique la construction d’une plateforme pour éviter que le drone ne nous détruise ou de détruise lui même lors des tests.
—————————– Article en cours de rédaction —————————–


